Programme du concours Droit-Économie d'admission en première année

Article 1 - Le concours Droit-économie porte sur le programme suivant :

Épreuves d'admissibilité

Composition sur un sujet d'ordre économique

1. Microéconomie

1.1 Mécanismes de marché

- Définition et description des structures de marché ;

- concepts d'offre et de demande du marché ;

- équilibre du marché et efficacité ;

- notion d'élasticité.

1.2 Comportements individuels

- Éléments de théorie du consommateur : préférences, utilité, contrainte budgétaire, décision de consommation, effets de revenu et de substitution, courbe de demande individuelle, offre de travail et comportement d'épargne ;

- éléments de théorie du producteur en concurrence pure et parfaite : profits, coûts, demandes de facteurs de production, décision de production, courbe d'offre individuelle, équilibre de long terme.

1.3 L'équilibre de concurrence pure et parfaite

- Offre totale et demande totale ;

- définition de l'équilibre concurrentiel ;

- équilibre partiel ;

- surplus et perte sèche ;

- équilibre général en économie d'échange pure et en économie de production ;

- optimum social : critères de Pareto et de compensation, fonction de bien-être social, équité ; les deux théorèmes de l'économie du bien-être.

1.4 La théorie des jeux

- Description d'un jeu et de son fonctionnement ;

- équilibre de Nash. 

1.5 Les imperfections de marché

- Le monopole ;

- la concurrence oligopolistique ;

- la concurrence monopolistique ;

- les asymétries d'information ;

- les politiques de concurrence.

1.6  Les défaillances de marché et leur prise en compte

- Les externalités ;

- les biens publics.

2. Macroéconomie

2.1 Le cadre comptable de l'activité économique

- Les principes généraux de la comptabilité nationale et les comptes d'exploitation ;

- les tableaux synthétiques (TEE, TES) ;

- les agrégats et les identités comptables ;

- la balance des paiements et la position extérieure nette ;

- l'évolution des équilibres comptables de la France au cours des cinq dernières années.

2.2 L'économie sur le long terme : la croissance et ses théories

2.3 Marchés, comportements et équilibre macroéconomiques en économie fermée

- Le marché des biens et services et les comportements de consommation, d'épargne et d'investissement ;

- le marché du travail et les comportements d'offre et de demande de travail ; le chômage ;

- le marché de la monnaie et les comportements d'offre et de demande de monnaie ;

- l'équilibre macroéconomique classique et keynésien ;

- le modèle d'équilibre global et la théorie du déséquilibre ;

- anticipations rationnelles et équilibre macroéconomique.

2.4 Politique économique

- Principes généraux de la régulation conjoncturelle ;

- principes généraux de la politique structurelle ;

- politiques économiques en Europe.

2.5 Relations économiques et financières internationales

- Institutions et relations monétaires internationales depuis 1944 ;

- globalisation économique et financière, principaux faits et grandes tendances ;

- système monétaire et financier international ;

- principales théories du commerce international.

Composition de droit civil

1. Introduction générale au droit

- Les caractères de la règle de droit ;

- les grandes divisions du droit (droit privé-droit public, mixte, international) ;

- les sources du droit ;

- le domaine d'application de la règle de droit dans l'espace et dans le temps ;

- l'interprétation ;

- les bases de l'organisation juridictionnelle ;- les droits subjectifs et leurs principales classifications ;

- la preuve des droits subjectifs ;

2. Le droit des personnes

- La personnalité juridique, définition, attributs, distinction personne physique et   morale ;

- les éléments d'identification des personnes physiques ;

- les droits de la personnalité ;

- la capacité et les incapacités ;

- les régimes de représentation (majeurs, mineurs) ;

3. Les biens

- Les droits réels et droits personnels ;

- le patrimoine ;

- les classifications des biens : meubles et immeubles, biens corporels et incorporels et autres classifications secondaires ;

- le droit de propriété : caractères et évolution, prérogatives et limites ;

- la possession ;

- les modes d'acquisition de la propriété (à l'exclusion de l'organisation et de la publicité foncière) ;

- les propriétés collectives (à l'exclusion de la copropriété des immeubles bâtis)

- les servitudes ;

- les relations de voisinage.

4. Les obligations

- les sources des obligations ;

- le contrat : la formation, les effets du contrat, l'inexécution et la responsabilité contractuelle ;

- les quasi-contrats ;

- la responsabilité extracontractuelle ;

- les deux principaux régimes spéciaux de responsabilité : la responsabilité du fait des véhicules terrestres à moteur, la responsabilité du fait des produits défectueux ;

Composition de droit commercial et de droit des sociétés

1. Droit commercial

- Les actes de commerce et les actes mixtes (notion et régime) ;

- les commerçants : définition, accès à la profession et obligations professionnelles ;

- les fonds de commerce : éléments du fonds, nature juridique, la propriété commerciale ;

- les opérations portant sur le fonds de commerce : vente, nantissement, gérances.

2. Droit commun des sociétés

- la formation des sociétés ;

- le fonctionnement de la société ;

- la dissolution de la société.

3. Droit spécial des sociétés

- les groupements non personnifiés (hors groupes de sociétés) ;

- les sociétés de personnes ;

- les sociétés de capitaux (dont la SARL).

Composition de droit public

1. Droit constitutionnel

1.1 Théorie générale du droit constitutionnel

- les éléments constitutifs et les formes de l'État ;

- l'organisation du pouvoir dans l'État.

1.2 Le constitutionnalisme : la Constitution (écrite ou coutumière, rigide ou souple) et le contenu du bloc de constitutionnalité

1.3 Le principe de séparation des pouvoirs et son application : régimes parlementaire,  présidentiel et mixte

1.4 La participation des citoyens (la démocratie), les élections, le référendum

1.5 Les institutions politiques françaises

- l'histoire constitutionnelle française depuis 1875 ;

- la Constitution de la Ve République.

2. Droit administratif

2.1 Les sources du droit administratif

- Les sources internes ;

- les traités internationaux.

2.2 L'organisation administrative

- L'administration d'État ;

- les collectivités locales ;

- les établissements publics ;

- les autorités administratives indépendantes, les autorités publiques indépendantes ;

- les rapports entre les personnes publiques : centralisation, décentralisation et déconcentration.

2.3 L'action de l'administration

- Le principe de la légalité administrative ;

- l'objet de l'action de l'administration ;

- les actes de l'administration, actes administratifs unilatéraux et contrats administratifs ;

- la responsabilité administrative extracontractuelle.

2.4 La justice administrative

- Les principales juridictions administratives ;

- le partage des compétences entre les juridictions administrative et judiciaire, le tribunal des conflits ;

- les recours gracieux et contentieux.

Exercices de mathématiques appliquées, statistiques et probabilités

1. Raisonnement et vocabulaire ensembliste

1.1  Éléments de logique

Les étudiants doivent savoir :

- utiliser correctement les connecteurs logiques « et », « ou » ;

- utiliser à bon escient les quantificateurs universel, existentiel et repérer les quantifications implicites dans certaines propositions et, particulièrement, dans les propositions conditionnelles ;

- distinguer, dans le cas d'une proposition conditionnelle, la proposition directe, sa réciproque, sa contraposée et sa négation ;

- utiliser à bon escient les expressions « condition nécessaire », « condition suffisante » ;

- formuler la négation d'une proposition ;

- utiliser un contre-exemple pour infirmer une proposition universelle ;

- reconnaître et utiliser des types spécifiques de raisonnement : raisonnement par disjonction des cas, recours à la contraposée, raisonnement par l'absurde, raisonnement par récurrence ;

- utilisation des symboles ∑ et ∏ ;

- changements d'indices.

1.2 Ensembles

- Ensemble, élément, appartenance ;

- sous-ensemble (ou partie), inclusion ;

- ensemble P (E) des parties de E ;

- réunion. Intersection ;

- complémentaire. Complémentaire d'une union et d'une intersection ;

- produit cartésien.

2. Généralités sur les suites

2.1 Généralités

- Définitions, notations ;

- exemples de définitions par formules récursives ou explicites, par restriction d'une fonction de variable réelle aux entiers ;

- étude du sens de variation d'une suite. 

2.2 Suites usuelles : formes explicites

Suite arithmétique, suite géométrique.

2.3 Convergence d'une suite réelle

- Limite d'une suite, définition des suites convergentes ;

- généralisation aux limites infinies ;

- unicité de la limite ;

- opérations algébriques sur les suites convergentes. Compatibilité du passage à la limite avec la relation d'ordre ;

- existence d'une limite par encadrement ;

- théorème de la limite monotone.

3. Fonctions réelles d'une variable réelle

3.1 Limite et continuité d'une fonction en un point

- notion de limite en + ∞ ;

- limite en - ∞ ;

3.2 Compléments sur les fonctions usuelles

3.2.1 Fonctions polynomiales, polynômes :

- degré, somme et produit de polynômes ;

- exemple des polynômes du second degré : discriminant, factorisation, signe ;

- limites en ±∞

3.2.2 Fonctions racine carrée, fonction inverse

Définition, notations, propriétés, règles de calcul, représentations graphiques.      

3.2.3 Fonctions logarithme et exponentielle

- théorème des croissances comparées : comparaison des fonctions exponentielles, puissance et logarithme au voisinage de +∞ et des fonctions puissance et logarithme au voisinage de 0 et +∞.    

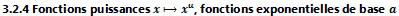
Définition, notations, propriétés, représentations graphiques. Limites aux bornes.

Définition, notations, propriétés, représentations graphiques. Limites aux bornes.

3.3 Étude globale

- fonctions majorées, minorées, bornées ;

- fonctions monotones ;

- théorème de la limite monotone ;

- fonctions continues sur un intervalle. Opérations algébriques, composition ;

- théorème des valeurs intermédiaires ;

- l'image d'un intervalle (resp. un segment) par une fonction continue est un intervalle (resp. un segment).

3.4 Dérivation

3.4.1 Définition, opérations

- taux d'accroissement. Dérivée en un point. Tangente au graphe en un point. Fonction dérivable sur un intervalle, fonction dérivée ;

- opérations sur les dérivées : linéarité, produit, quotient, fonctions puissances. Dérivée des fonctions composées ;

- caractérisation des fonctions constantes et monotones par le signe de la dérivée ;

- extremum local d'une fonction dérivable.

3.5 Intégration

3.5.1 Définition

- aire sous la courbe d'une fonction positive ;

- primitive d'une fonction continue sur un intervalle. Toute fonction ƒ continue sur un intervalle admet, sur cet intervalle, au moins une primitive F;

- théorème fondamental de l'analyse ;

- intégrale d'une fonction continue sur un segment ;

- relation de Chasles.          

3.5.2 Propriété de l'intégrale

Linéarité et positivité de l'intégrale. L'intégrale d'une fonction positive sur un segment est positive. L'intégrale d'une fonction continue et positive sur un segment (non réduit à un point) est nulle si et seulement si la fonction est identiquement nulle sur le segment.

3.5.3 Techniques de calcul d'intégrales

- primitives usuelles (lecture inverse des formules de dérivation) ;

- intégration par parties.

3.5.4 Intégrales généralisées

- convergence d'une intégrale généralisée (ou impropre) d'une fonction continue sur un intervalle semi-ouvert ou ouvert ;

- cas d'une fonction définie sur un intervalle et continue sur cet intervalle sauf éventuellement en un nombre fini de points ;

- linéarité, positivité, relation de Chasles ;

- critère de comparaison des intégrales de fonctions positives ;

- convergence absolue ;

- la convergence absolue implique la convergence.       

4. Étude élémentaire des séries

4.1 Séries numériques à termes réels

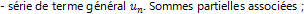
- définition de la convergence. Combinaison linéaire de séries convergentes ;

- convergence absolue ;

- la convergence absolue implique la convergence.       

4.2 Séries numériques usuelles

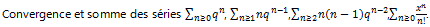
5. Combinatoire

      

6. Probabilités sur un univers fini

6.1 Événements
- expérience aléatoire. Univers Ω ;

- événements, événements élémentaires, opérations sur les événements, événements incompatibles ;

- système complet d'événements fini.

6.1.1 Probabilité

- définition d'une probabilité sur P(Ω) ;

- propriétés d'une probabilité :

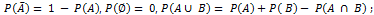
- cas de l'équiprobabilité.   

6.1.2 Probabilités conditionnelles

- probabilités conditionnelles ;

- formule des probabilités composées ;

- formule des probabilités totales.

6.1.3 Indépendances d'événements

- indépendance de deux événements.

7. Variables aléatoires discrètes

7.1 Variables aléatoires 

- définition de la loi d'une variable aléatoire quelconque ;

- indépendance de variables aléatoires ;

- définition d'une variable aléatoire discrète à valeurs dans R;

- la somme, le produit de variables aléatoires discrètes sont des variables aléatoires discrètes ;

- caractérisation de la loi d'une variable aléatoire discrète par la donnée des valeurs P(X=x) pour x∈ X(Ω)

- fonction de répartition d'une variable aléatoire. Propriétés ;

- loi d'une variable aléatoire ;

- variable aléatoire Y=g(X), où g:X(Ω). Étude de la loi de Y=g(X).

7.2 Couple de variables aléatoire, indépendance

- lois de probabilité d'un couple de variables ;

- représentation dans un tableau (cas où X(Ω) et Y(Ω) sont finis) ;

- lois marginales, lois conditionnelles ;

- indépendance de deux variables aléatoires discrètes.

7.3 Lois discrètes usuelles

- loi certaine ;

- loi uniforme sur un ensemble fini E, sur {1;...;n). Loi de probabilité, espérance, variance de U(n);

- loi de Bernoulli B(p) ;

- loi Binomiale B(n;p). Loi de probabilité, espérance, variance ;

- loi géométrique (temps d'attente d'un premier succès dans un processus de Bernoulli sans mémoire). Espérance et variance ;

- loi de Poisson : espérance, variance.

8. Variables aléatoires réelles à densité

8.1 Généralités

- situations où l'univers image de X est un intervalle ou une réunion d'intervalles non réduits à un point ;

- définition d'une variable aléatoire à densité ;

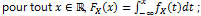
8.2 Espérance d'une variable aléatoire à densité :

- espérance. Variables centrées ;

- linéarité de l'espérance ;

- loi uniforme sur un intervalle. Espérance ;

- loi exponentielle. Espérance ;

- loi normale centrée réduite ;

- loi normale (ou de Laplace-Gauss). Espérance ;

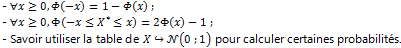
9. Statistiques simples et doubles

9.1 Statistiques simples

- définition d'une variable statistique : population, caractères, modalités. Effectifs, fréquence ;

- les caractéristiques de position (mode, médiane, quantiles, moyenne) et de dispersion (variance, écart-type, intervalle interquartile). Représentations graphiques.

9.2 Statistiques doubles

- nuage de points ;

- covariance et coefficient de corrélation ;

- qualité de l'ajustement ;

- ajustement affine par la méthode de la droite des moindres carrés.

Composition de langue vivante étrangère

Cette épreuve ne comporte pas de programme (voir l'arrêté relatif aux conditions d'admission).

Épreuves d'admission

Interrogation orale sur un sujet d'ordre économique

Le programme de cette épreuve est le même que celui de la composition d'ordre économique.

Interrogation orale sur un sujet d'ordre juridique

Le programme de cette épreuve est le même que celui de la composition de droit civil.

Interrogation orale de langue vivante étrangère

Cette épreuve ne comporte pas de programme (voir l'arrêté relatif aux conditions d'admission).

Épreuve orale d'entretien

Cette épreuve ne comporte pas de programme (voir l'arrêté relatif aux conditions d'admission).

 

Article 2 -  L'article 4 de l'arrêté du 28 novembre 2014 modifié susvisé, relatif aux programmes des concours d'admission en première année et des concours d'admission en cycle master de l'École normale supérieure de Rennes est supprimé.

 

Article 3 -  Les dispositions du présent arrêté entrent en vigueur à la session 2020 du concours.

 

Article 4 -  La directrice générale de l'enseignement supérieur et de l'insertion professionnelle et le président de l'École normale supérieure de Rennes sont chargés, chacun en ce qui le concerne, de l'exécution du présent arrêté, qui sera publié au Bulletin officiel de l'enseignement supérieur, de la recherche et de l'innovation.

 

Fait le 18 avril 2018